John Blagrave was a mathematician, geographer, land surveyor and instrument maker living in London in the second half of the seventeenth century. In 1585 he wrote a book called The Mathematical Jewel, which was printed in London by Walter Venge. The Mathematical Jewel ambitiously promised its readers to “leadeth any man practising thereon, the direct pathway (from the first steppe to the last) through the whole Artes of Astronomy, Cosmography, Geography, Topography, Navigation, Longitudes of Regions, Dyalling, Sphericall Triangles, Setting figures, and briefly whatsoever concerneth the Globe or the Sphere”. In practice, the book explained how to make and use a particular kind of navigational instrument: a new kind of astrolabe, which Blagrave named “The Mathematical Jewel”.
Gabriel Harvey owned one copy of this book, now in the British Library (C.60.o.7.). His copy of the book is, characteristically of Harvey, covered with annotations. One of these quotations, “Schollars haue thir bookes: & practitioners thr Learning” points out the simultaneous “bookishness” of this book and its role as an instrument for practitioners.

The Jewel isn’t just a musty book to be perused by the bespectacled scholar: it also demands a particularly active kind of reading. It does this by giving its readers instructions on how to make a version of the Mathematical Jewel for themselves. The titles of some of these instructions – “How to place the fixed starres in the Reete” (B4v) – conjure up an image of a reader becoming a kind of divinely inspired Creator of a papery universe. But paragraphs of text – broken up by inert, schematic diagrams – struggle to convey the lively, intricate three-dimensional process by which the reader must mark out meridians and angles.

What conveys this making process much more clearly, in this copy, is the attempt of one reader (possibly Harvey himself) to have a go at following the instructions. In among the printed contents pages are some interleaved sheets which display a hand-drawn paper instrument. The reader here has transformed the instructions given in the text into a three dimensional, useable, Mathematical Jewel complete with rotating pin.
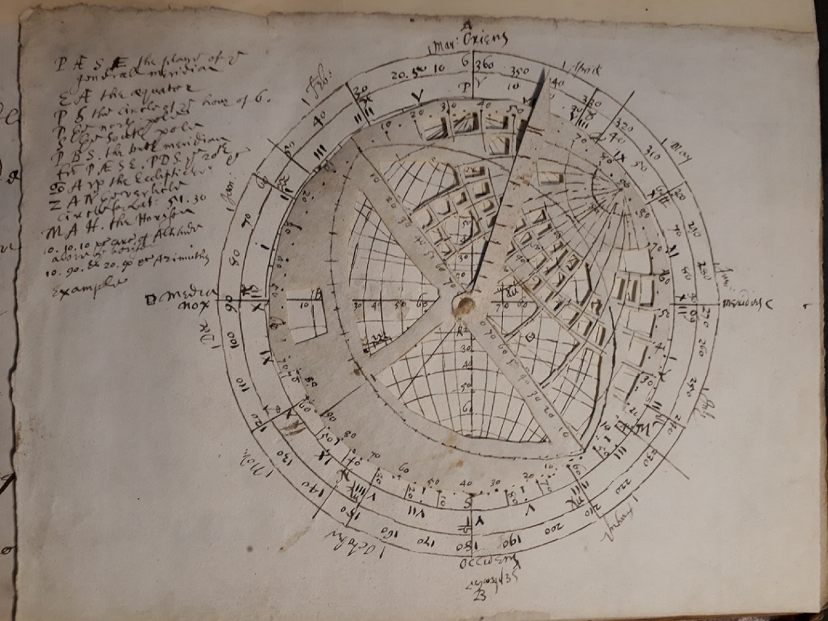
This copy also contains part of the printed instrument stuck out and pasted onto a leaf in the book – and a replica of that part by hand. But as a single layer unattached to any moving parts this is only a half-formed instrument: a single stage of the process is captured and preserved in the print and the drawing. We can see below the hand-drawn version how the reader has written out the instructions to themselves for the instrument, using letters to mark points and calculate distances.
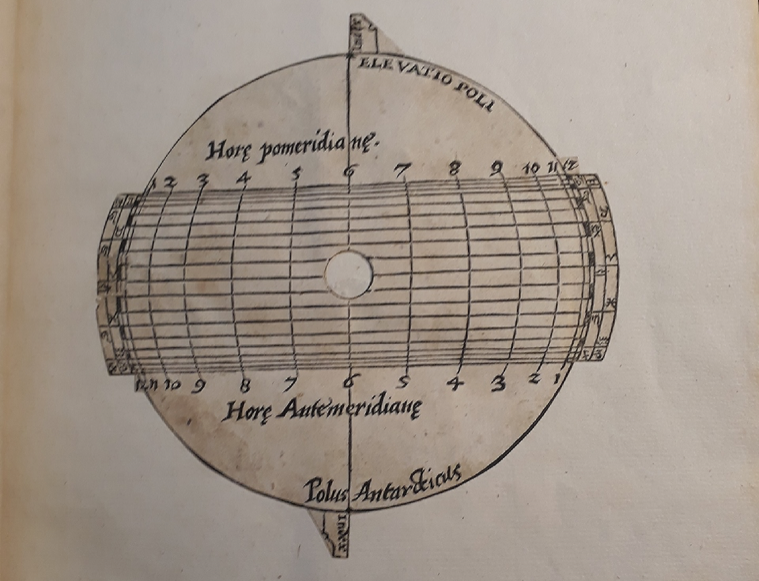

Whilst the paper instrument in this copy is a three-dimensional creation which springs from the printed text, the Mathematical Jewel grapples with projecting the machinations of the universe onto a flat surface. Blagrave himself doubts the truthfulness of such a representation: “there is no affinitie or proportion of a straight line to a crooked, nor of a globe to a plaine; therefore there resteth no other meane to bring this purpose to effect but only by the art Opticke, commonly called Prospective” (B2v). Despite this book’s claims to usefulness ad accuracy, was the flattening out of three dimensions onto two just a deceptive – if aesthetic – optical illusion?
