Visualisation in Modern Geometry

The most substantial obstacle in describing modern Geometry, sometimes even to other mathematicians, lies in its unrelenting emphasis on ‘higher dimensional spaces’. What does it mean to say we can construct a shape if we can’t describe what it looks like? In what sense does it exist? These are the kind of philosophical questions mathematicians generally elide in their work, but pose a genuine challenge to mathematical exposition. I will try and outline a couple of ways in which geometers do in fact ‘see’ higher dimensional shapes, either by projecting them to smaller dimensions, or producing diagrams which serve as a blueprint for the higher dimensional space.

First I should give a hint of the kind of objects geometers work with. By way of a simple example, if you take any number of co-ordinates we can always form the set of points where the sum of the squares of the co-ordinates equals one. This object is always called a sphere (and a circle when there are just two co-ordinates), and now you have a whole collection of shapes of different dimensions. We can also think about the region inside the sphere, called a ball. It turns out that even spheres, in some sense an extremely simple shape, can hold surprises and rich structures.

Objects which are ‘smooth’, like spheres, are of particular interest to geometers, and are called manifolds. Such objects turn out to be simple and fundamental enough to support a beautiful theory, and yet exhibit many rich and remarkable properties. However, what can it mean to ‘see’ such an object? Moreover what is the purpose of doing so, since mathematical logic tells us we should never need to draw a picture to prove something rigorously? Certainly in general terms we can say that visualisation engenders insight and intuition for a problem, using which technical tools can be used to prove theorems. More than this though, the process of visualisation often creates new geometric objects which either leads to new theories or relates existing ones, often in fruitful ways.

Figure 1. A three dimensional ball with three handles attached.

One beautiful example of this process of visualisation is the use of handlebodies in topology. By a fundamental result in Morse theory any smooth four dimensional space can be constructed from a (four dimensional) ball by a process of attaching handles. The handles themselves are higher dimensional versions of ‘tubes’, and come in a few flavours, the simplest ‘1-handles’ are formed by taking a three dimensional ball and ‘extending’ it in the fourth direction (rather like forming a tube by starting from a disc in a horizontal plane and extending it vertically). These handles are glued on to the boundary of the ball, which is a three dimensional sphere. The analogous picture one dimension lower is shown in Figure 1.

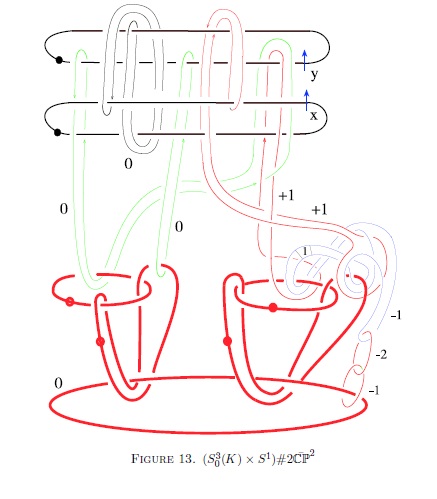
Figure 2. Example of a handlebody picture.

While even a three dimensional sphere is hard to visualise, if you remove a point from the sphere we can identify the resulting space with usual three dimensional space. Thus we can describe constructions of interesting four dimensional objects from diagrams drawn in three dimensions, by indicating where the handles are attached. Since certain types of higher dimensional handles are glued along knots in the three-dimensional space, one can use complicated knots to describe extremely interesting four dimensional shapes, for example Figure 2, taken from recent work of Akbulut (2015) on the visualisation of a certain exotic four manifold.

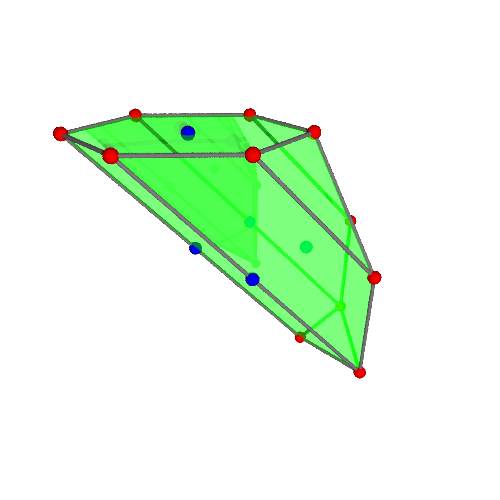
A second example of visualisation in geometry, close to my own research, comes from toric geometry. In toric geometry one considers certain 2n-dimensional shapes which are constructed from an n-dimensional ‘model’ or projection. In this context then a three dimensional object is used to reconstruct a six-dimensional one! The n-dimensional models are quite a different type of geometric object: a polytope. Unlike manifolds, polytopes are formed by joining together polygons in three dimensional space to form the faces of a three dimensional body. Some examples are familiar (cubes, tetrahedra, and the other platonic solids) but, as shown in Figure 3, they need not be at all regular.

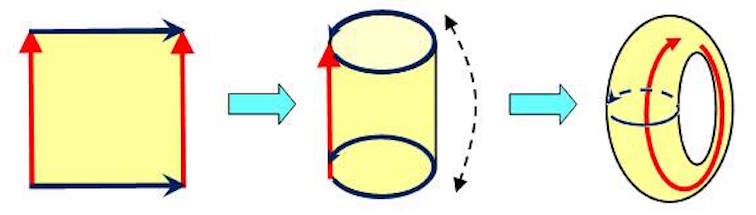
The construction of a 2n-dimensional ‘smooth’ object from a polytope is easier to visualise in lower dimensions. The simplest example of this process would simply take a line segment as the polytope. We attach a circle to each point of the line segment, forming a cylinder, and then shrink these circles to single points at the ends of the segment, forming a sphere. This is one way of constructing a two dimensional shape (a sphere) from a one dimensional one (a line segment).

"Figure 4. Gluing a torus together." — Figure 4. Gluing a torus together.

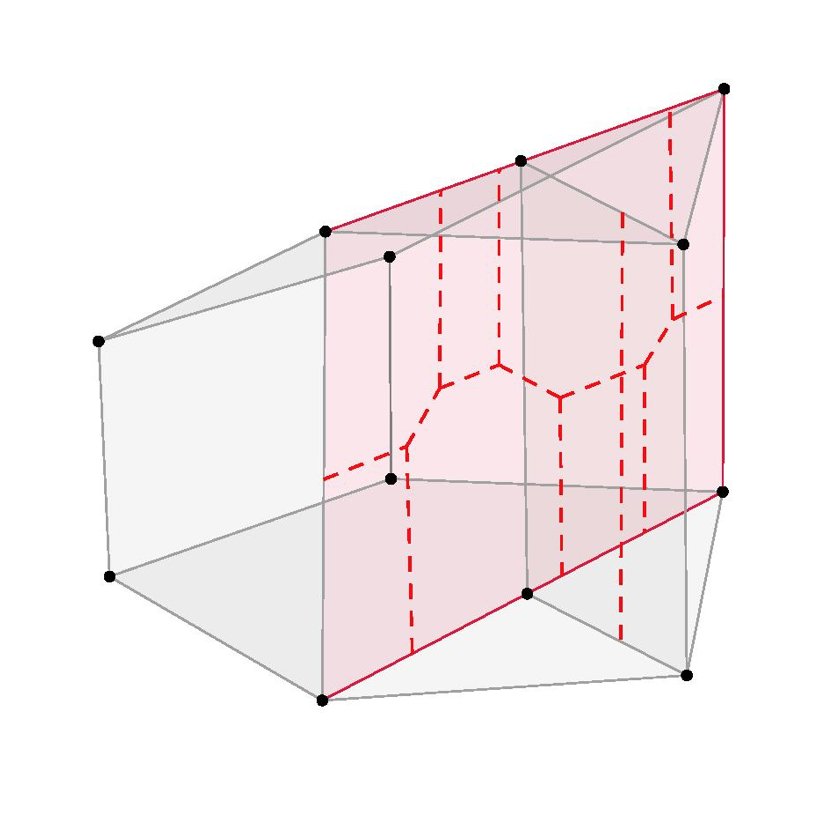
If instead of a line segment we choose a polygon, a square or a triangle for example, we can apply a similar process. Rather than attaching a circle at each point we attach a torus (the ‘doughnut’ shape formed by gluing the top to the bottom, and the left to the right edges of a square, as shown in Figure 4. As we move to the edges the tori shrink down to circles, and near the vertices they shrink down to points. To check the total dimension of this shape we add the dimension of the base to the dimension of the general (torus) fibre, both of which are equal to two.

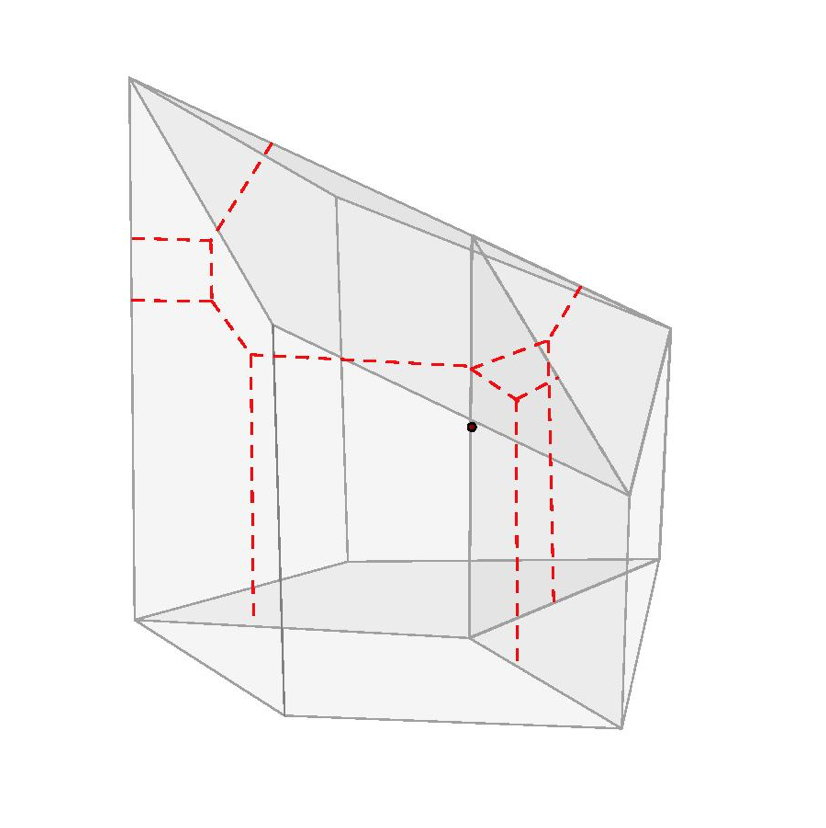
The three dimensional analogue of this construction has played a key role in my research: one constraint of toric geometry is that you only recover a small proportion of interesting shapes in any given dimension from the construction described. My work recently has been based on a generalisation of this construction, in which rather than just attaching tori of different dimensions the tori are allowed to ‘pinch’ or degenerate in some way. This makes the base structure more complicated, no longer a polytope, but allows one to access a broader range of spaces. I have included some figures from this project, visualising interesting six-dimensional spaces. Roughly, the additional data consists of the red curves, which indicate where the usual torus fibres that project to each point need to degenerate to certain kinds of singular tori.

Further reading