Sebastiano Serlio (Bologna 1475 - Fontainebleau 1554) was a virtuoso of spatial representation through applying “linee occulte” or hidden lines. Serlio’s knowledge culminated in rhetoric architectural drawings by applying these lines. This, so the lines represent hidden connections by drawing geometrically following Neoplatonic thinking (Hersey, 1976, 81-87; Hart & Hicks, 1996, 458). For Serlio, architecture needs taught first by geometry and subsequently by the study of perspective. Unsurprisingly, the two first books are the books on geometry and perspective. Despite this, the books were published in a bilingual edition in 1545, a few years later than the fourth book on the orders (Regole Generali, 1537), and the third book on antiquities (Le Antiquità di Roma, 1540). In these books Serlio outlined the importance of geometry and perspective for the architect, without which “the architect would be unable to produce anything worthwhile” (Serlio, Hart, 1996, 3). Such knowledge on geometry and perspective manifested itself through drawing, indicating Serlio’s principle of linee occulte relates to the architectural drawing. Thus, Serlio developed linee occulte as technical tools for drawing ‘hidden’ geometries whilst at the same time used them as judicious instruments, for making reasoned decisions.
Evidently linee occulte relate to Alberti’s principle of “lineamenta,” or lineaments. Such lineaments have been described as derived from the mind and relate to all lines and linear characteristics in design (Alberti, Rykwert, Leach, & Tavernor, 1988, 422-23). Here, lineaments belong to the intellect, and differ from “materia” or worldly matter (Alberti, Rykwert, Leach, & Tavernor, 1988, 7). In contrast stands Serlio’s linee occulte, which connect mind and matter, making linee occulte distinct from lineaments. This is evident in book VI where Serlio used “lineamenti” to describe the lines outlining the layout of the gardens as seen in figures 1 and 2 (Serlio, Hart & Hicks, 1996, 196).

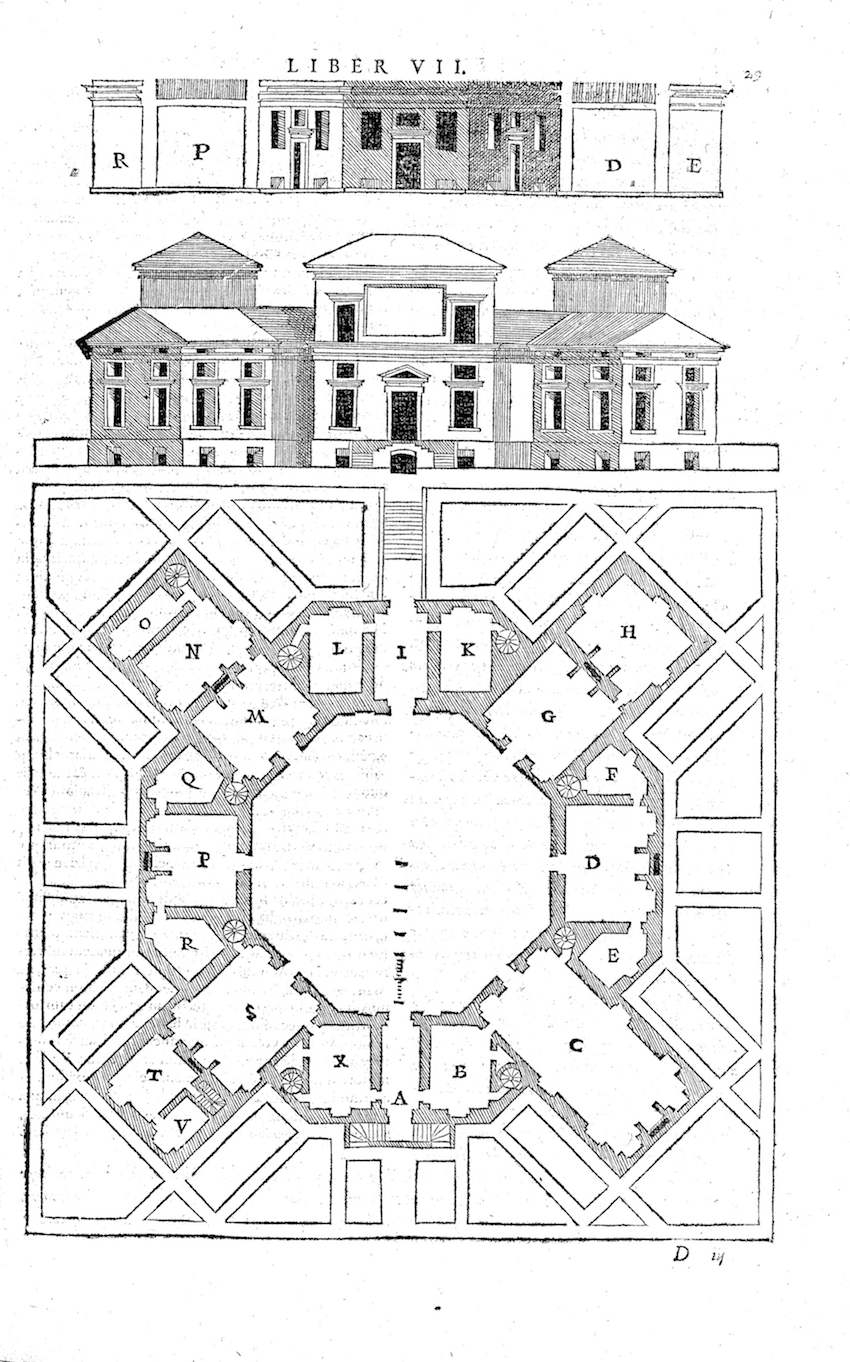
First, this denotes Serlio’s awareness of Alberti’s lineaments. Second, this implies Serlio used lineaments for perceivable lines. This is the opposite of linee occulte which are to be erased when being drawn in order to become “hidden.” Linee occulte, are thus an intrinsic part of the drawing process in which the hidden (occulte) differ from the perceivable (evidenti) (Serlio, Hart & Hicks, 1996, 457-459). The difference between linee occulte and linee evidente is clear in figures 3 and 4, where the dotted lines depict hidden geometry, whilst the solid lines are the ones seen. As such, linee occulte are the method for creating an architectural representation. This is apparent throughout books one and two were linee occulte are mostly mentioned as constructive tools (Serlio, Hart & Hicks, 11, 42, 50, 51, 52, 56, 64, 66, 70, 72, 76).
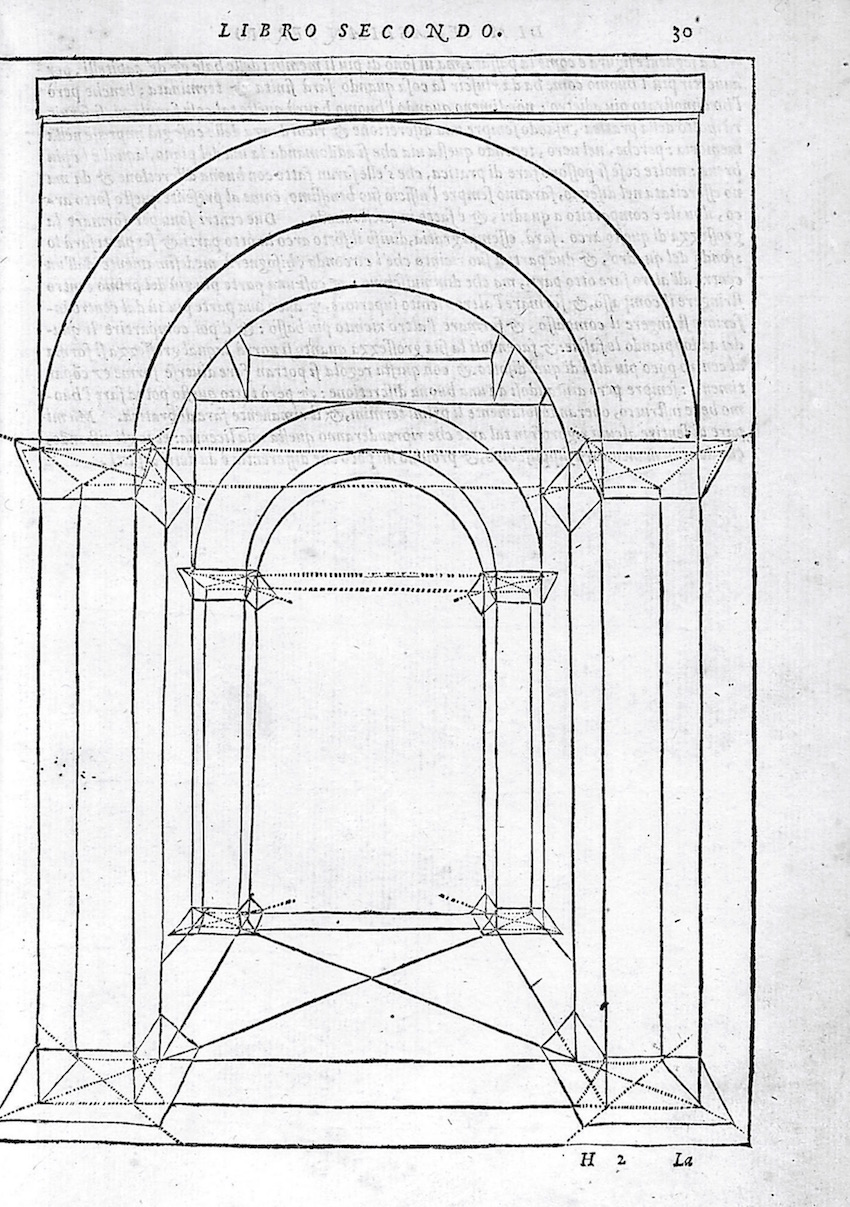

Beyond tools for drawing, evidence suggest linee occulte are also theoretic. For instance, Serlio explains that the outer appearance of lineaments gives less insight in architecture than the geometric study of hidden parts (Serlio, Hart & Hicks, 1996, 48). Then Serlio elaborates; “once a man is acquainted with … hidden parts, … [he] will make many things with a practice which, however, will have originated with theory” (Serlio, Hart & Hicks, 1996, 48). Hence, linee occulte narrate architectural concepts due to its embeddedness in theory. However, when looking to the work of Serlio, it is not only the mathematical but also the ornamental that is important. This can be seen when looking at the elaborate flooring pattern in figure 4. Thus, every architectural representation consists of the ornamental and the mathematical. The ornament pleases the modal observer, whilst, its mathematics are only distillable by the initiates of linee occulte. Moreover, linee occulte were the ideal instrument for creating spatiality, making the architectural representation more communicative and comprehensible. As a case to point this out, figure 5 shows one of Serlio’s licentious gates in which the spatiality is analysed by looking into the perspectival linee occulte. No other hidden geometries will be analysed. The gate is exemplar since Serlio described it as a “disguised and masked” Doric gate in which “the columns are unfinished [rusticated] but their measurements are nonetheless present” (Serlio, Hart & Hicks, 2001, 468). In the same Extraordinary Book Serlio mentions that “it seems evident that even for the most licentious inventions, its hidden geometry can be deduced” (Serlio, Hart & Hicks, 2001, 461).

Striking about this figure are its ornaments, as they are partially used to suggest spatiality. By using linee evidenti, Serlio simulates spatiality in a two-dimensional drawing by adding shadow, material and depth. For instance, the shadows are insinuated by using horizontal, vertical or inclined lines. Coarse and rusticated materials are suggested by rough shortly curved and whimsically, yet carefully, orchestrated lines. Last, depth is represented through shadows which to outline curvature, progressions and regressions from the surface. However, depth is also suggested by applying perspective which can be seen by looking at the steps, the door, the voussoirs and the cornice. Thus, Serlio’s skill in architectural representation comes forth, namely linee evidenti are wielded to suggest spatiality. Yet, less evident is the role linee occulte play in representing spatiality. For this a perspectival analysis of the gate is required. This is done by applying LiDAR (Light Detection and Ranging), a remote-sensing technology which three-dimensionally scans surfaces transmitting data in point-clouds. When imported into CAD (Computer-Aided-Design) software the format of the data is vectorial, and thus mathematical. This allows a more mathematically accurate analysis of geometry and perspective in comparison to conventional hand-measuring. The process of going from the scan to a CAD emulation can be seen in figure 6.

Figure 7 shows a CAD emulation of the perspective as derived from the laser-scan. The lines do not converge in one vanishing-point. However, these fallacies can be explained when taking-into-account the inaccuracy resulting from printing and cutting the xylograph. Further, as the measure and scale of the perspective lines are very small, a distortion can easily be drawn in the reconstruction. This is particularly the case at the bottom, where the perspectival mismatch is biggest. More interesting is that Serlio used several vanishing-points for the construction of the initial drawing. The reasons for this can be explained by looking into figure 8. Here a one point-perspective is simulated by applying one central vanishing-point at the approximate eye-level. This perspective would work well for the upper part of the drawing, with the exception of the voussoirs which are more distorted in comparison to the original design. Due to the distortion there is less space for the ornamental which are required to please patrons. The ornamental is nonetheless important for these gates, as Serlio wanted to ‘satisfy everyone’ particularly when one wanted to be ‘different from everyone else’ (Serlio, Hart, & Hicks, 2001, 468). At the bottom of the gate, the distortion of the steps would be so big, they would draw to much attention, creating a discord in the composition.
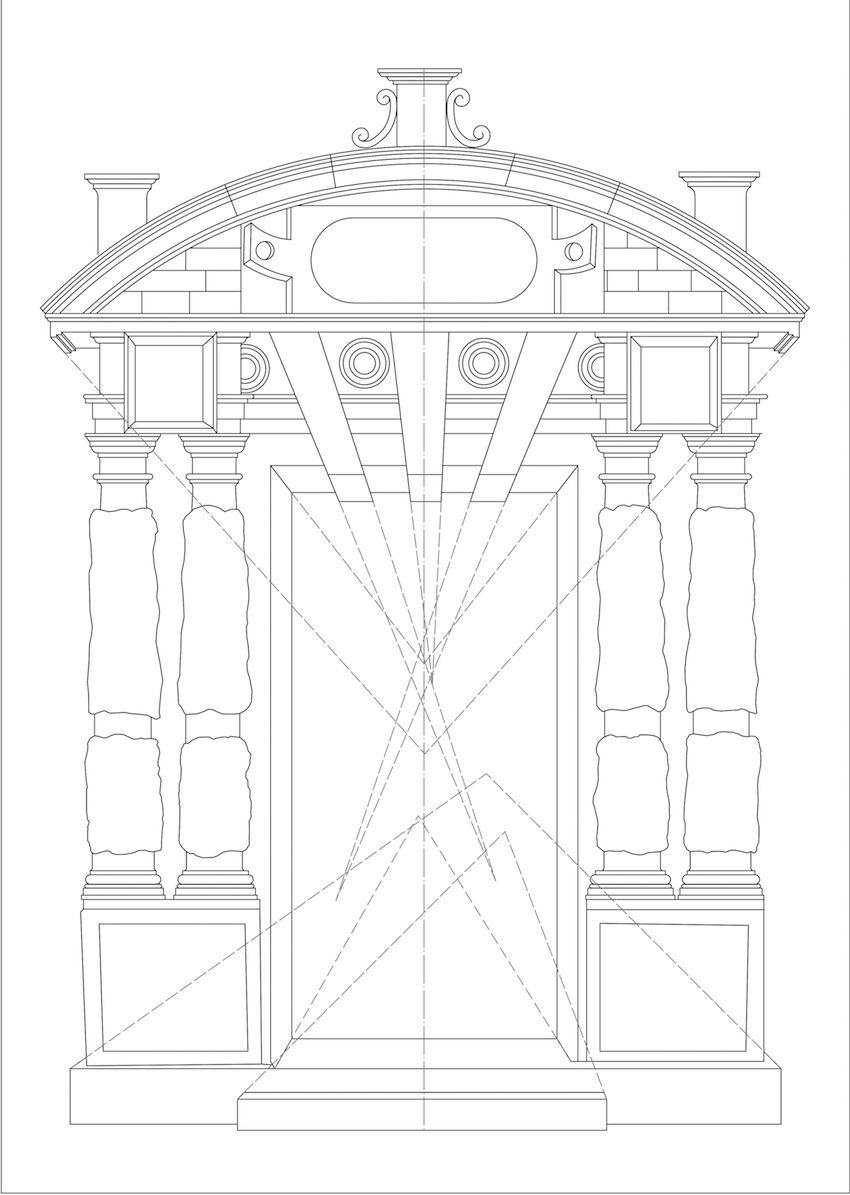
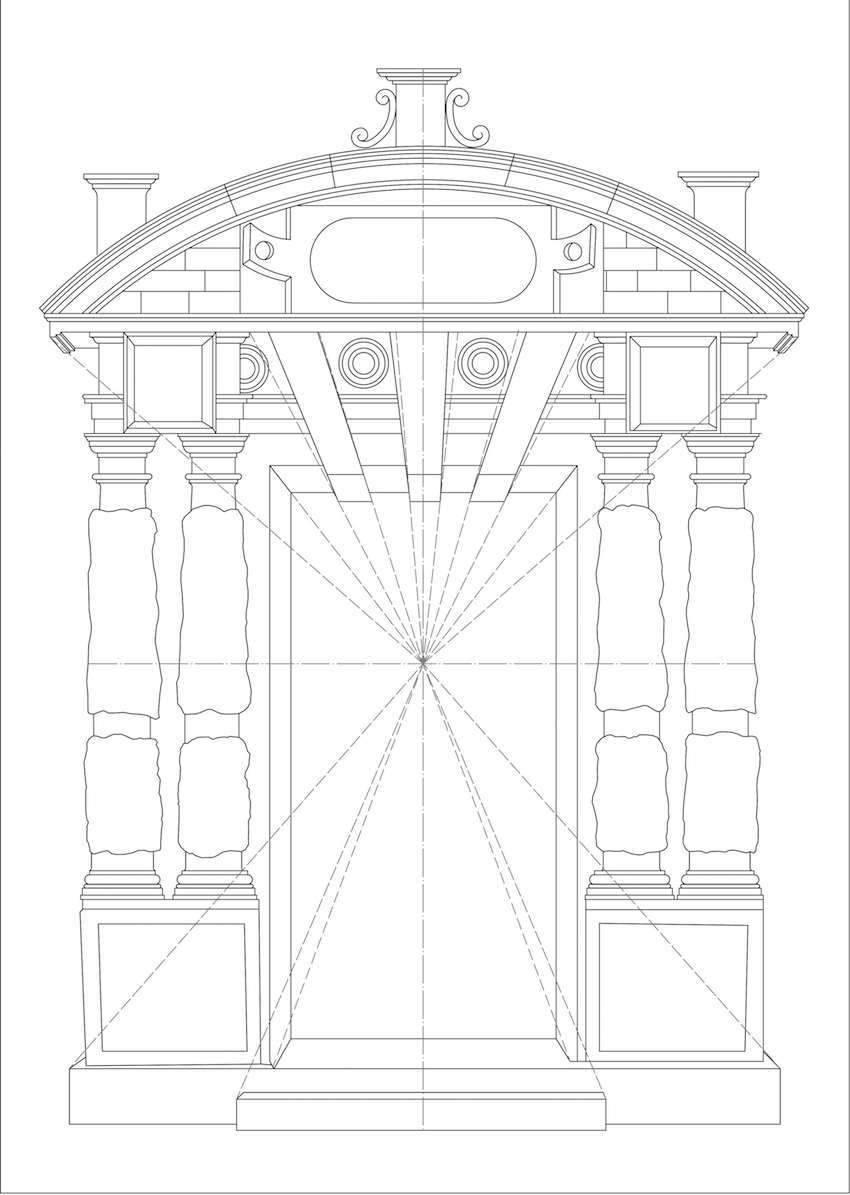
Serlio explains two methods for drawing an architectural perspective (see figure 9), but, he uses neither method for the construction of the gate. This is not surprising as Serlio also explains that licence can be taken if need be, repositioning the vanishing-point for a better effect. Serlio even uses several vanishing-points if required but always “with the assistance of good judgement” (Serlio, 1566, 27-28, 31). Further the erroneous methods of Serlio have already been outlined, but, Serlio himself endorses his errors stating, “I can well imagine, however, that some purists in this art, would reproach the liberty taken by me” (Serlio, Hart, & Hicks, 1996, 31). Thus, when Serlio takes licence from perspectival rules, he does this for the representative effect and takes-into-account the perception of the audience.

This sheds new light on Serlio’s gate constructions. Figure 10, depicts perspectival linee occulte in the easiest possible way, having two vanishing-points positioned on a central axis. The results in a drawing which resembles the original composition. Here, the discord at the bottom is resolved, but the voussoirs are still not distorted through which the roundels cannot be depicted properly. For drawing the roundels clearly, the voussoirs need distorting. This is achieved by adding more vanishing-points at the lowermost horizon as can be seen in figure 11. Unsurprisingly, this ‘optimised’ perspective resembles the original composition of Serlio, best.

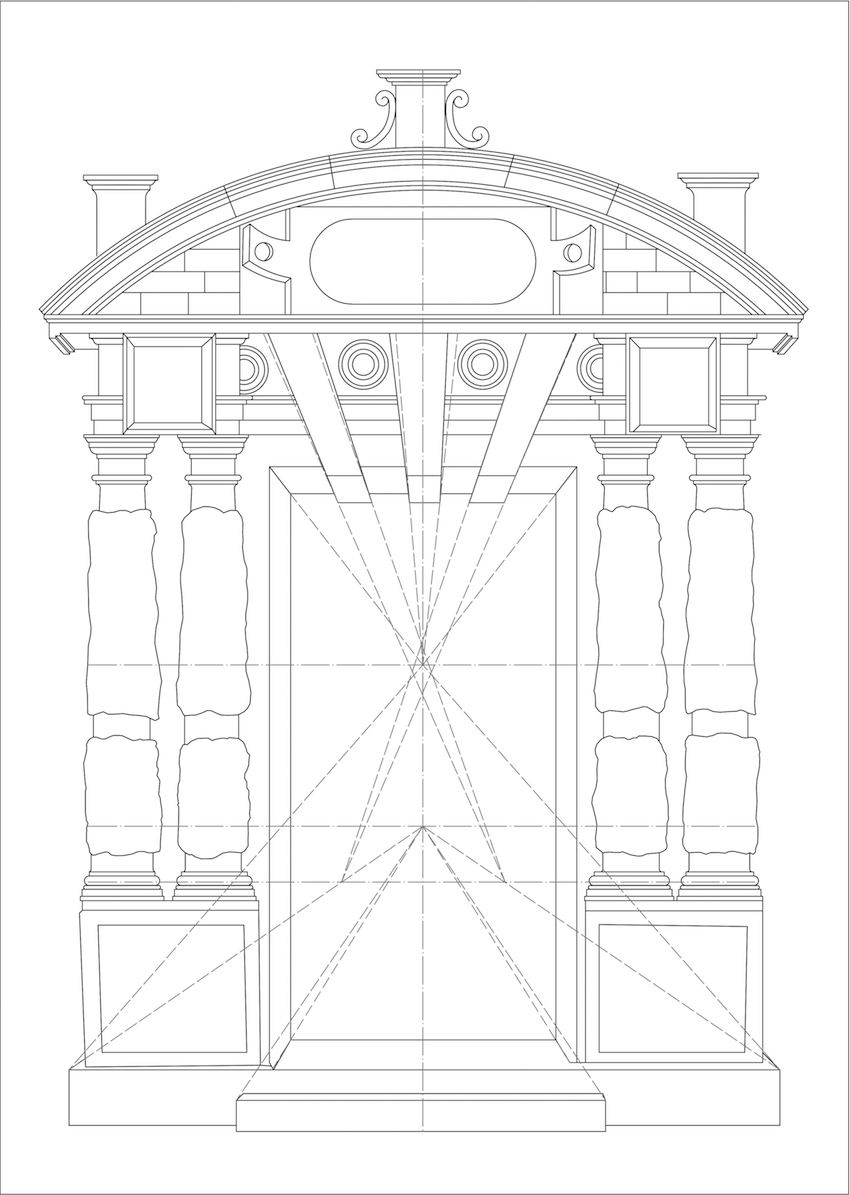
To conclude, Serlio used several vanishing-points in his designs, knowingly renouncing correct mathematical applications. This shows he was aware of more complex perspectival applications than book two suggests. Serlio allowed the amending of methods to create the desired effect which was most didactic to the eye of the beholder. Nonetheless, such amendments were based on mathematical reasoning to visualise spatiality. Endorsing such a mathematical constitution in the most licentious book of Serlio is remarkable. For every single design, however ornate these might look, mathematical reasoning lies at the basis and was done through linee occulte. Thus, hidden lines were not only a mean for drawing, but also rhetoric ones as it relied on reason. Hence, Serlio can be considered a virtuoso of spatial representation. A representation perceivable by linee evidenti but always conveyed by linee occulte.
Further Reading:
Alberti, Leon Battista, On the Art of Building in Ten Books, translated by Joseph Rykwert, Neil Leach, Robert Tavernor (Cambridge Mass., London: The MIT Press, 1988), 422-3.
Damisch, Hubert, The Origin of Perspective, translated by John Goodman (Cambridge Mass., London: The MIT Press, 1994):
Emmons, Paul, Drawing Imagining Building: Embodiment in Architectural Design Practices (Abingdon: Routledge, 2019).
Hersey, George, Pythagorean Palaces: Magic and Architecture in the Italian Renaissance (Ithaca: Cornell University Press, 1976).
Kemp, Martin, The Science of Art, Optical Themes in Western Art from Brunelleschi to Seurat (New Haven, London: Yale University Press, 1990), 87.
Onians, John, Bearers of Meaning; The Classical Orders in Antiquity the Middle Ages, and the Renaissance (Princeton: Princeton University Press, 1988), 263-309;
Serlio, Sebastiano, Regole generali di architettura (Venice: Francesco Marcolini, 1537).
Serlio, Sebastiano, Il Terzo Libro (Venice: Francesco Marcolini, 1540).
Serlio, Sebastiano, Le premier livre d’architecture… Le Second livre de perspective mis en langue francoyse par Iehan Martin (Paris: Jean Barbé, 1545).
Serlio, Sebastiano, Libro Primo-Quinto d’Architettura (Venice: Francesco Senese & Zuane Krugher, 1566).
Serlio, Sebastiano, On Architecture, translated by Hart Vaughan, Peter Hicks, volume 1 (New Haven, London: Yale University press, 1996).
Serlio, Sebastiano, On Architecture, translated by Hart Vaughan, Peter Hicks, volume 2 (New Haven, London: Yale University press, 2001).
Temple, Nicholas, Disclosing Horizons, Architecture, Perspective, and Redemptive Space (Abingdon: Routledge, 2007), 129.
