The Premier tome tome de l’architecture is the first comprehensive architectural treatise written in the French language and one of the most fascinating theoretical texts of its time (Fig. 1). Philibert de L’Orme (1514–70) composed it at the end of an extraordinary career during which he rose from the ranks of stonecutter to the office of surveyor of the royal works under King Henri II (1547–59) as one of the most celebrated architects of his time.Among the many features that make the Premier tome a truly original work within the panorama of sixteenth-century architectural theory is de L’Orme’s discussion of stereotomy in Books III and IV (Fig. 2).

Stereotomy is the art of cutting stones into particular shapes for the construction of vaulted structures. The art is best known for a variety of acrobatic masterpieces produced in early modern France, such as Jules Hardouin-Mansart’s composite vault in the Town Hall of Arles (Fig. 3). However, stereotomy is neither early modern nor European; it has been practiced over a wide chronological span, from Hellenistic Greece to contemporary Apulia, and across a broad geographical range, centered on the Mediterranean Basin but reaching far beyond — including the British Isles, Armenia and the Caucasus, as well as colonial Central America. Stereotomy is also known for a substantial body of theory that started with the treatises of architects such as de L’Orme and Alonso de Vandelvira (1544–1625) and engaged practitioners and mathematicians alike in a heated debate throughout the eighteenth century. By focusing on the geometry of solids, this body of theory also crucially contributed to the definition of Gaspard Monge’s theory of descriptive geometry, the branch of mathematics concerned with the two-dimensional representation of three-dimensional objects.

De L’Orme was not the first author to write about stereotomy — Villard de Honnecourt (ca. 1230), Pedro de Alviz (ca. 1550), and Hernán Ruiz el Joven (ca. 1550), among others, had included stereotomic problems in their manuscripts. However, de L’Orme was the first to attempt an ambitious theory of stereotomy by giving systematic form to a comprehensive corpus of case studies. Moreover, de L’Orme’s choice to print his material and to include it in a broader treatise on architecture made it available to a much wider audience than the circles of initiated professionals to whom stereotomy treatises like Vandelvira’s Libro de trazas (ca. 1585) were addressed. This editorial choice made de L’Orme’s the best known of sixteenth-century texts on stereotomy.

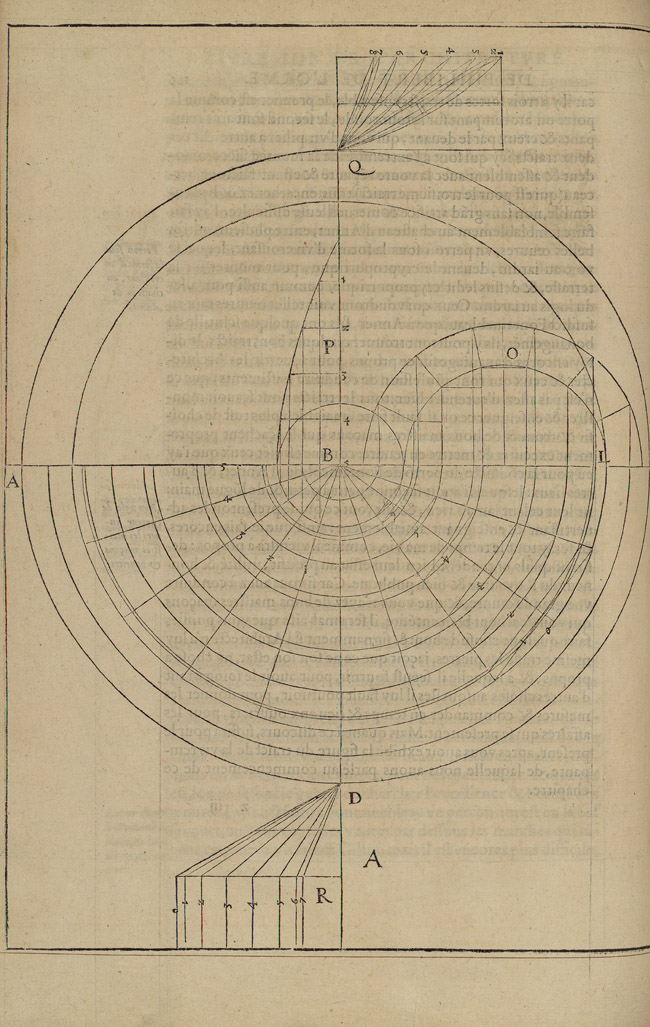
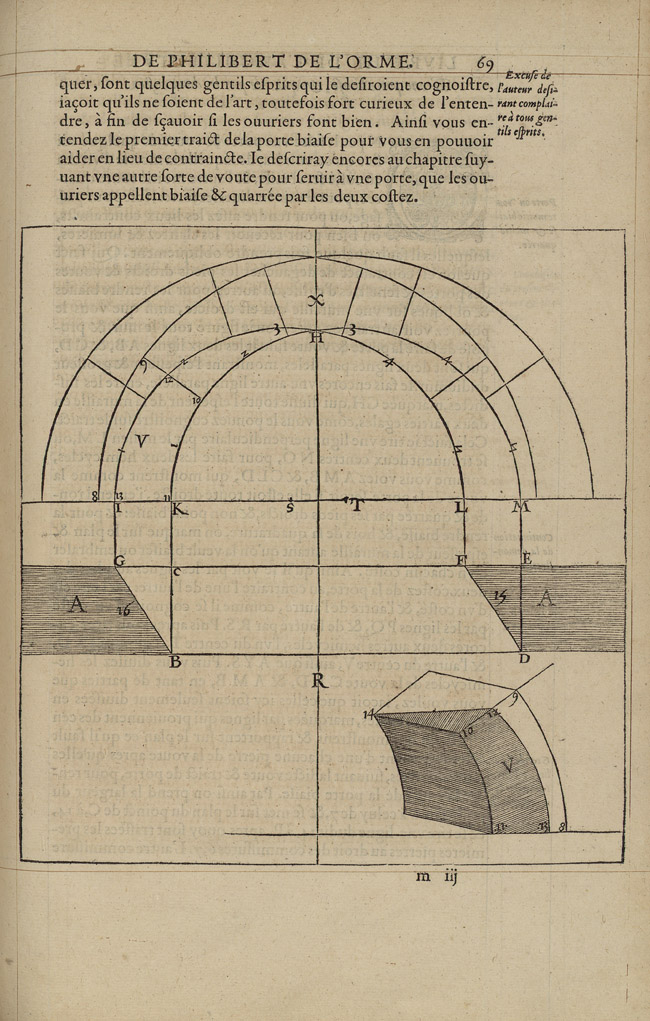
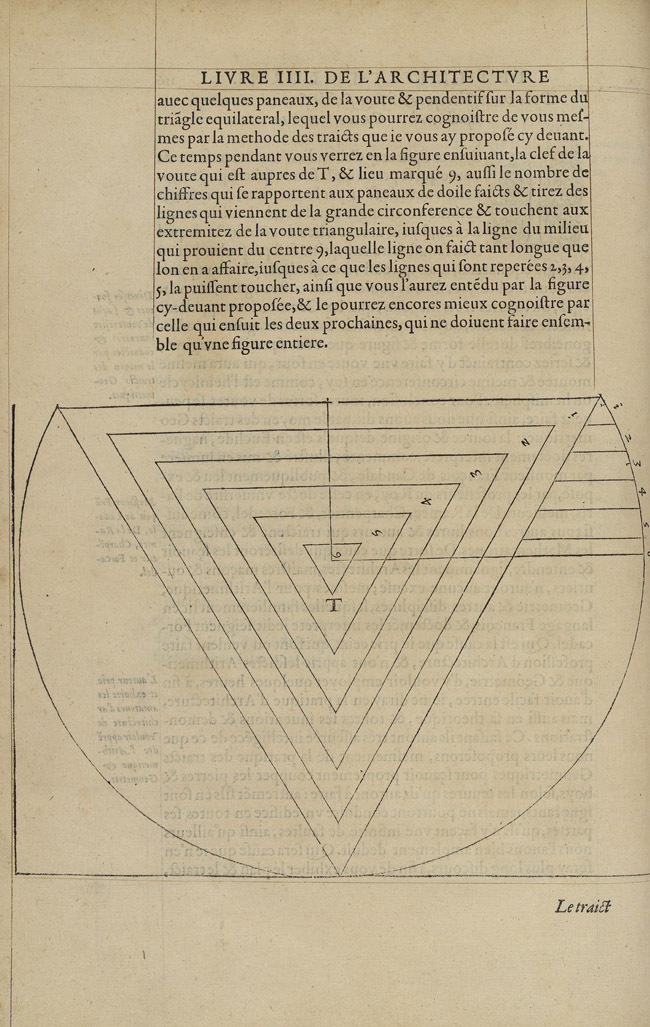
Books III and IV of the Premier tome illustrate 32 case studies, 27 of which are dedicated to stereotomic vaulted structures, three to rib vaults (including one made of wood), and two to spiral staircases. Combined, the two books comprise 79 folios and include 51 illustrations, 30 of which in full-page format. The vaulted structures are organized in 11 typologies that include inclined barrel vaults, skew and corner arches, arches inserted in curved walls, groin vaults, domes, trumpet vaults, and helical barrel vaults (Figs 4 and 5).
The geometric complexity of the selected case studies dictates their order of appearance, from the simplest—the inclined barrel vault—to the most complex, the helical barrel vault of the Vis de Saint Gilles type. The same applies to the variants presented for each type. In the section dedicated to arches that open in curved walls, for instance, de L’Orme first illustrates a standard model — a round arch opening in a curved wall (Fig. 6) — and then proceeds to illustrate less common examples featuring skew arches opening in curved and inclined walls (Figs 7 and 8).
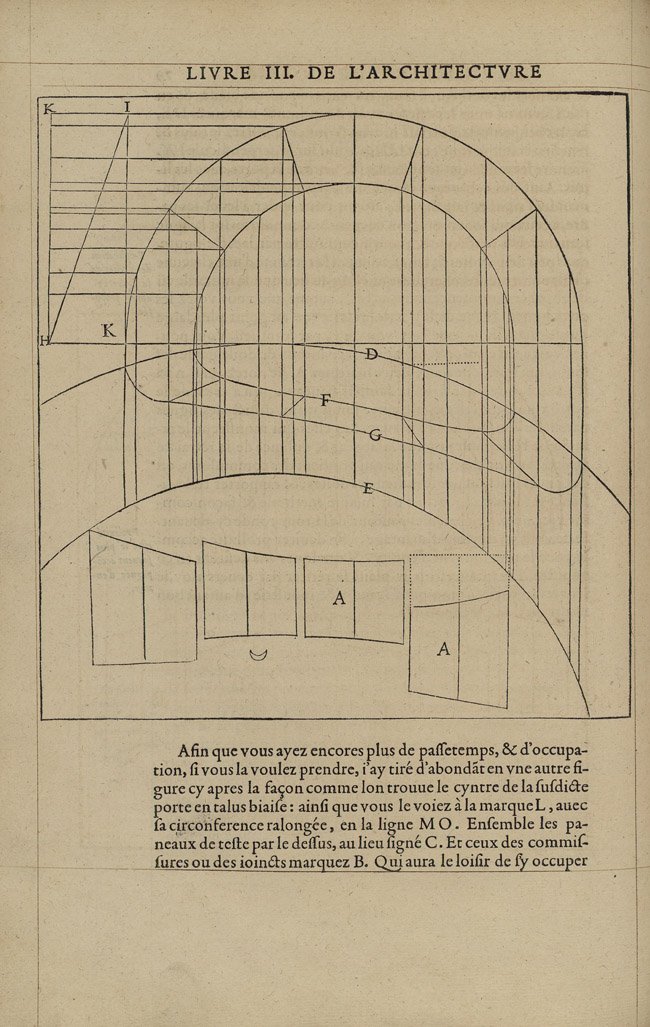
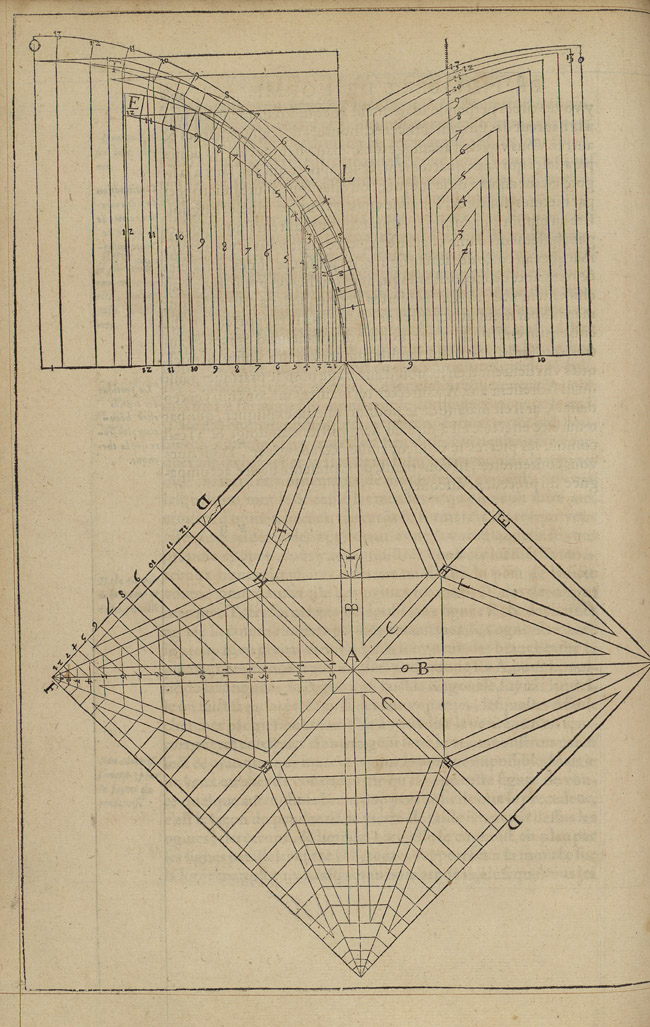
Some notable exceptions to this organizing principle are the inclusion of case studies that pose little or no stereotomic challenge, such as the above-mentioned rib vaults (Fig. 9). These exceptions reflect the broader scope of the Premier tome, which trumps, at times, the internal logic of the section dedicated to stereotomy. Rib vaults were still largely in use in de L’Orme’s time and, as vaults made of stone, they fit the chapters dedicated to stereotomy better than any other section of the treatise.
De L’Orme makes it clear that his material on stereotomy derives directly from practice. Yet the modes and implications of the vaults’ translation into paper models are far from obvious. Contrary to what readers may expect, there is in fact no direct correspondence between the vaults de L’Orme built and those he includes in the treatise. Quite to the contrary, the author’s selection of vaults clearly indicates that Books III and IV were not intended as a catalogue of his own oeuvre but, rather, as a corpus of case studies derived from a broad range of practices. A case in point: of the many stereotomic vaults de L’Orme designed during his career, only one is illustrated in the Premier tome: the trumpet vault of the Château d’Anet (Fig. 10).

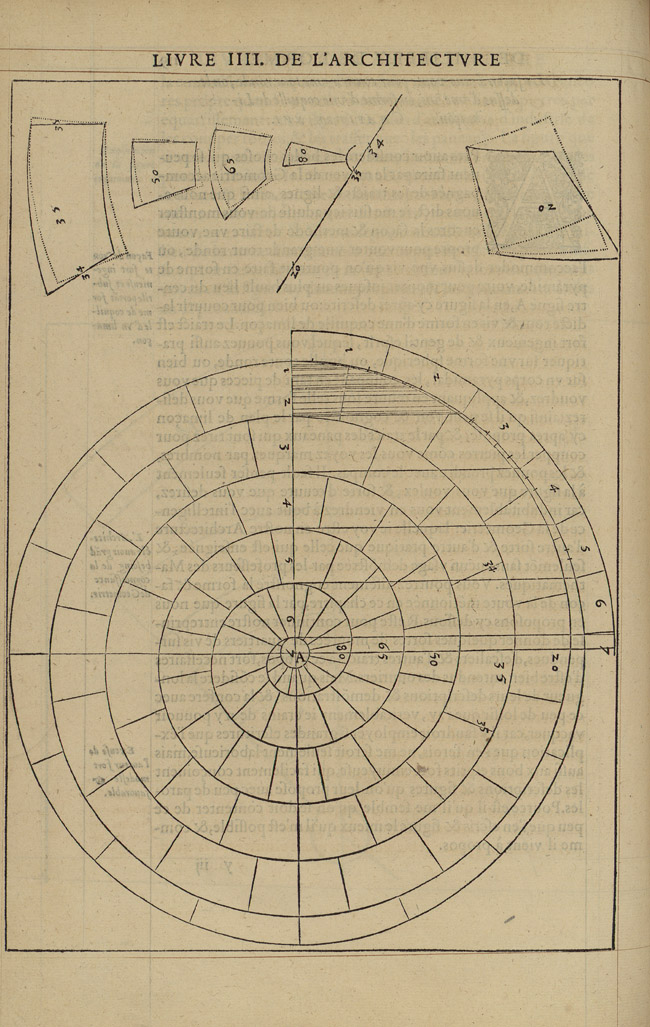
On the other hand, the treatise features vaults de L’Orme has never employed in his buildings, as well as vaults with which the architect was visibly unfamiliar and for which he produces incorrect geometric constructions, such as the dome featuring a single, helical course (Fig. 11).
It is also of note that de L’Orme does not illustrate the standard models of many of the vault types he deals with in Books III and IV, such as the semi-spherical dome with horizontal courses, the most common type of stereotomic dome and one that is abundantly featured in other treatises. Instead, de L’Orme indulges in the illustration of eccentric types, such as domes featuring rectangular and triangular plans and non-horizontal stone courses (Figs 12 and 13). He explicitly identifies the function of these extravagant models as theoretical—that is, their inclusion affords him more latitude for theoretical exploration. At the beginning of the section on trumpet vaults, for instance, he writes (Premier tome, fol. 89v):
A trumpet vault can be built on a right, obtuse, or acute angle, and it can take any form one wishes in elevation: straight, projecting square, half a hexagon or octagon, or round. And one can build straight, concave, or rampant trumpet vaults or vaults of any type one can think of, depending on the needs and the constraints of the chosen site. All sorts of vaults can be built in the form of trumpets, and all of them can be built hanging in the air with no support on the ground other than on the side walls, all with the same method for tracing.
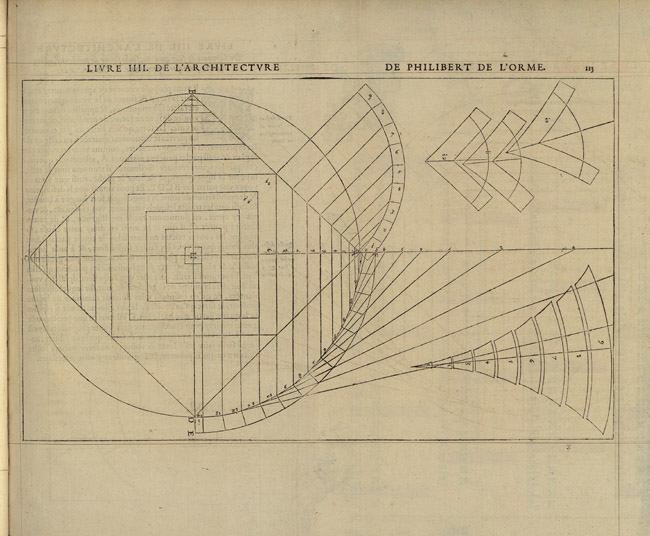
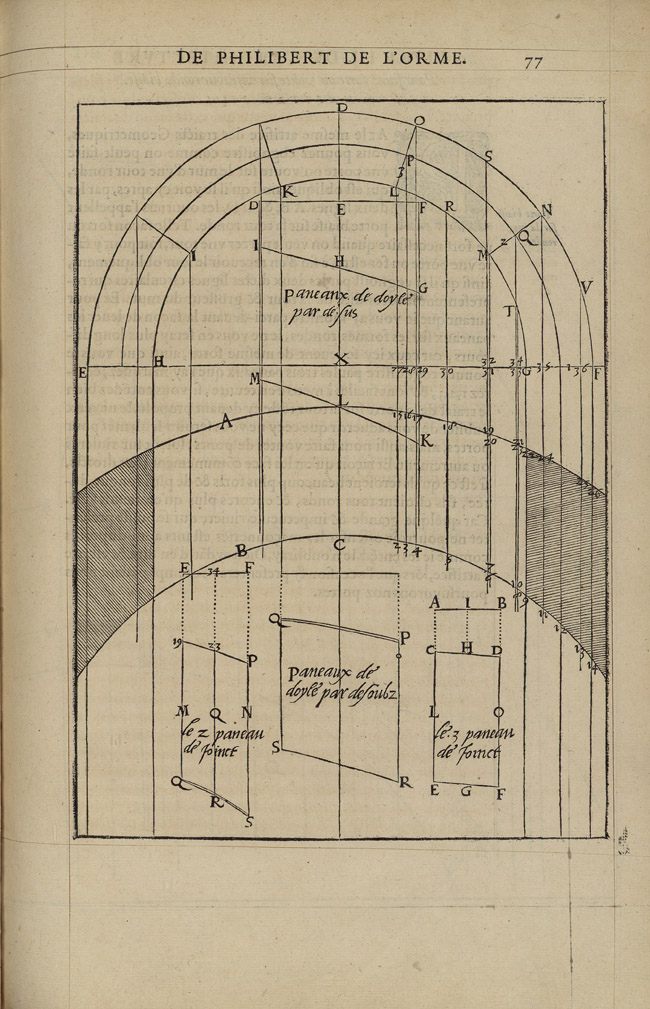
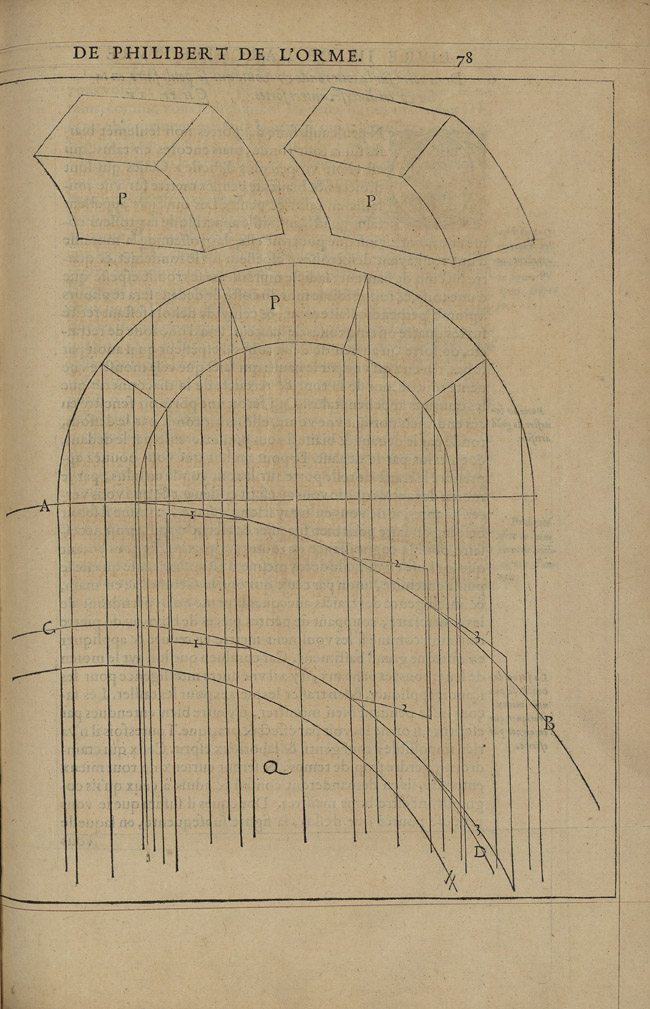
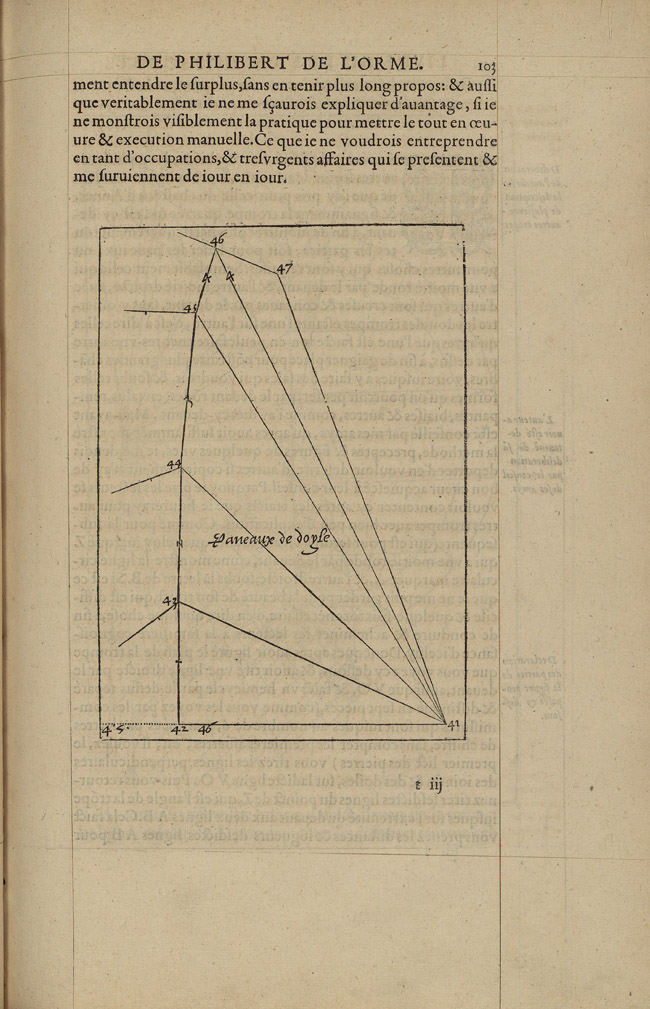
De L’Orme then proceeds to demonstrate this method by showing, through four case studies, that the épures of a trumpet vault—the geometric constructions necessary to obtain the 1:1 scale drawings of the sides of the voussoirs—are obtained through the same process no matter how extravagant its shape, because the geometric problem underlying all trumpet types, independently of their specific form, is the development of a conic surface (Figs 14 and 15).
The geometric constructions and methods illustrated by de L’Orme are of particular interest in the context of sixteenth-century mathematical knowledge and its dissemination. Books III and IV of the Premier tome not only demonstrate a number of triangulation and rotation methods that will be codified by Monge as tenets of descriptive geometry, but they also show geometric constructions that, in de L’Orme’s time, seem to have been unknown outside of the building trades.

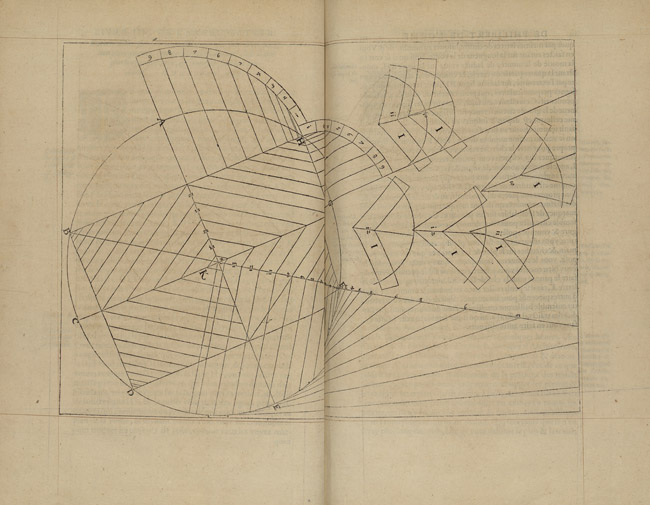
This is the case, for instance, of the conical-sectioning of the sphere that de L’Orme repeatedly shows in his chapters on domes, and which provides an alternative to the methods for the development of the sphere known by Renaissance cartographers (Fig. 16).
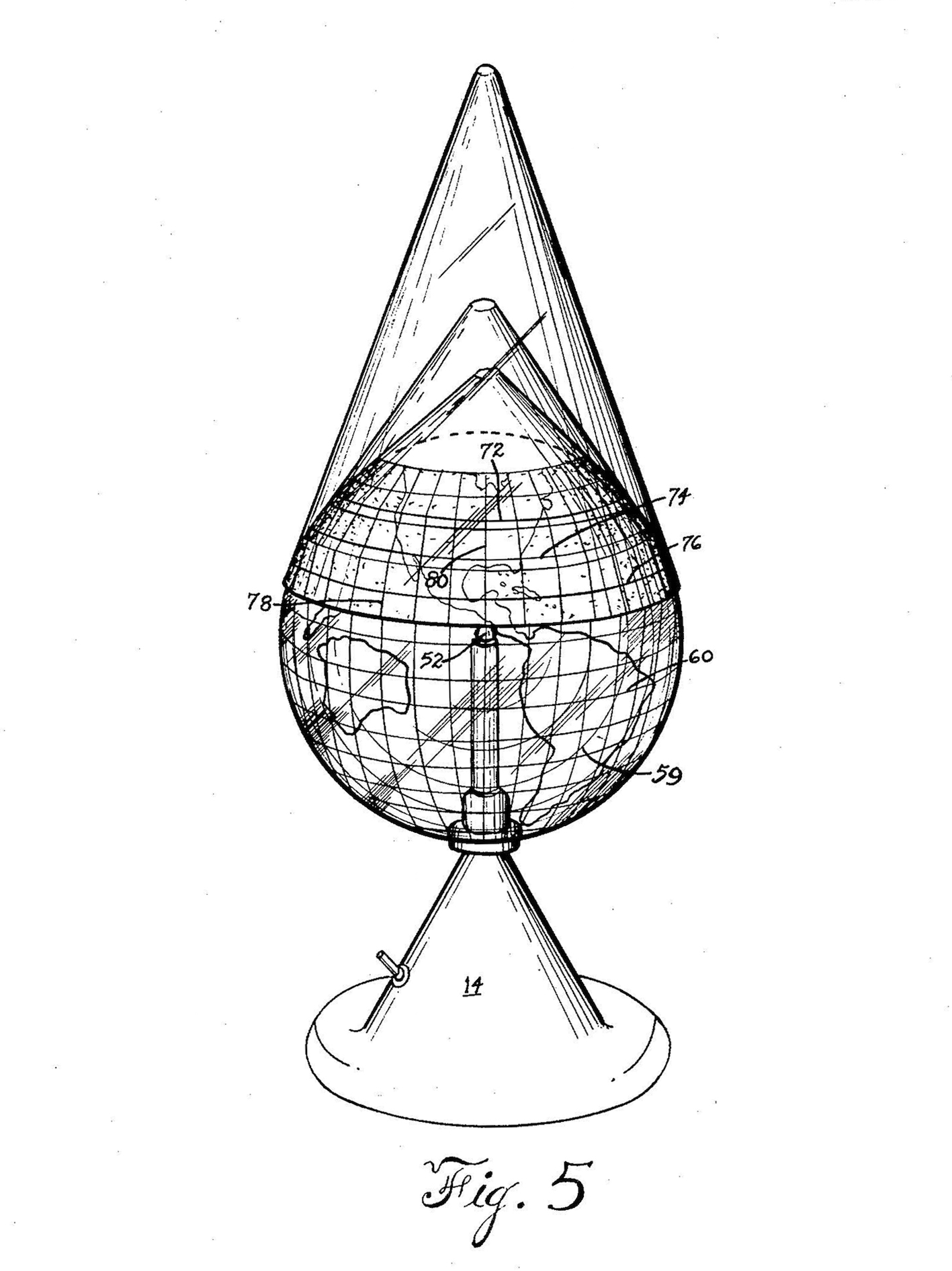
The method illustrated by de L’Orme was first introduced in the world of cartography by Ferdinand Hassler in 1825, and is known since as the American polyconic projection. It consists of viewing the sphere as composed by separate cone sections belonging to a series of stacked, overlapping cones (Fig. 17). The non-developable, doubly curved geometry of the sphere is thus simplified to that of a series of concentric cones, which can be developed. While sixteenth-century cartographers did not employ it, the tracings found in the Cathedrals of Seville and Murcia show that this method of developing the sphere was by then well known already among practitioners of stereotomy.
De L’Orme’s books on stereotomy are an ambitious attempt at theorizing one of the most fascinating and complex techniques in the history of pre-modern architecture. Some of the geometric constructions illustrated in his treatise were unknown to mathematicians of de L’Orme’s time, and the Premier tome was likely the means by which they were first introduced to a broad readership.
Further reading
José Calvo López et al., “The Tracing for the Sail Vault at the Murcia Cathedral Vestry: Surveying a 16th-Century Full-Scale Working Drawing,” International Journal of Architectural Heritage: Conservation, Analysis, and Restoration 7, 3 (2013), 275–302.
Sara Galletti, “From Stone to Paper: Philibert de L’Orme, the Premier tome de l’architecture (1567), and the Birth of Stereotomic Theory,” Aedificare: International Journal of Construction History 2 (2018): 143–62.
Sara Galletti, “Stereotomy and the Mediterranean: Notes Toward an Architectural History,” Mediterranea: International Journal on the Transfer of Knowledge 2 (2017), DOI: https://doi.org/10.21071/mijtk.v0i2.6716.
Sara Galletti, “Philibert de L’Orme’s Divine Proportions and the Composition of the Premier tome de l’architecture,” Architectural Histories 2, no. 1 (2014), Art. 12, DOI: http://doi.org/10.5334/ah.bh.
Ricardo Garcia Baño and José Calvo López, “Los recursos gráficos en el manuscrito de cantería atribuido a Pedro de Alviz (BNE MS 12686),” in Francisco Hidalgo Delgado and Concepción López González, eds., XI Congreso Internacional de Expresión Gráfica Aplicada a la Edificación (Valencia 2012), Valencia, Universidad Politècnica de València, 2012, 157–65.
Jean Guillaume, “Philibert de L’Orme: un traité different,” in Id., ed., Les traités d’architecture de la Renaissance: actes du colloque tenu à Tours du 1er au 11 Juillet 1981, Paris, Picard: 1988, 347–54.
Claude Lalbat, Gilbert Marguerite and Jean Martin, “De la stéréotomie médiévale: la coupe des pierres chez Villard de Honnecourt, I and II,” Bulletin monumental 145 (1987), and 147 (1989), 387–406 and 11–34 respectively.
Frédérique Lemerle and Yves Pauwels, eds, Philibert De l’Orme, un architecte dans l’histoire. Arts, sciences, techniques, Turnhout: Brepols, 2016.
Pedro Navascues Palacio, El Libro de arquitectura de Hernán Ruiz, el joven, Madrid, Escuela Técnica Superior de Arquitectura, 1974.
Yves Pauwels, “Les antiques romains dans les traités de Philibert De L’Orme et Jean Bullant,” Mélanges de l’École française de Rome. Italie et Méditerranée 106 (1994), 531–47.
Jean-Marie Pérouse de Montclos, Postface to Philibert de l’Orme, Traités d’architecture, Paris: Laget, 1988, 1–22.
Francisco Pinto Puerto, Las esferas de piedra: Sevilla como lugar de encuentro entre arte y ciencia del Renacimiento, Seville: Diputación de Sevilla, 2001.
José Antonio Ruiz de la Rosa, “Evolución de las tradiciones operantes en Arquitectura: el dibujo sobre soporte pétreo,” in Carlo Inglese and Antonio Pizzo, eds, I tracciati di cantiere: disegni esecutivi per la trasmissione e diffusione delle conoscenze tecniche, Rome: Gangemi, 2016.
Joël Sakarovitch, Épures d’architecture: de la coupe des pierres à la géométrie descriptive, XVIe-XIXe siècles, Basel: Birkhäuser, 1998.
John P. Snyder, Flattening the Earth: Two Thousand Years of Map Projections, Chicago: University of Chicago Press, 1993.
Fully digitised copy from the École nationale supérieure des Beaux-Arts, Paris is available here.
