Throughout the early modern period a key text, at least in learned circles, for thinking about three-dimensional things was the Elements of Geometry by the ancient mathematician Euclid. First printed in Latin in 1482 and in Greek in 1533, the text appeared in something close to three hundred different versions during the sixteenth, seventeenth and eighteenth centuries, as editors and printers responded to an insatiable demand not just for the Elements of Geometry but for new and improved takes on those elements.

The sixteenth-century French bishop François de Foix-Candale (1512–94) was not ostensibly the most likely person to be involved in this story. Descendant of a remarkable family including the ninth-century Dukes of Gascony and heroes of the Hundred Years’ War and of Agincourt (on the English side: Candale is ultimately a corruption of the Earldom of Kendal), he held minor ecclesiastical positions until taking over the bishopric of Aire, in Burgundy in 1578. But his first love was learning. His home held a chemical laboratory, where he attempted to produce ingots of silver and (more successfully) brewed an alcoholic ‘Eau de Candale’, effective against every malady. But his main public appearance was not as alchemist, pharmacist or indeed bishop, but as a geometer.

His Latin edition of Euclid’s Elements appeared at Paris in 1566. The dedication and preface declared a familiar set of agendas: the importance of geometry in training the mind, the importance of a pure and accurate text of the Elements which this editor alone could provide, based on a faithful collation of selected earlier versions. But by far the most obvious feature of this new Elements was the number of books it contained. Not the thirteen that Euclid, as far as we can discern, actually wrote, nor the fifteen that had become standard by the late antique period. But sixteen. François de Foix-Candale wrote an extra book.

His Book 16 was concerned primarily to expand upon the final few constructions of Book 15: in particular the sometimes complex and beautiful figures which resulted when one regular polyhedron was placed inside another. It considered, for example, a regular tetrahedron and a cube inscribed inside it. How large is the tetrahedron relative to the cube? (There are three possible anwers, depending on whether you consider the lengths of the edges, the diameters, or the volumes of the two figures. Foix-Candale studied them all.) It’s a virtuoso performance.
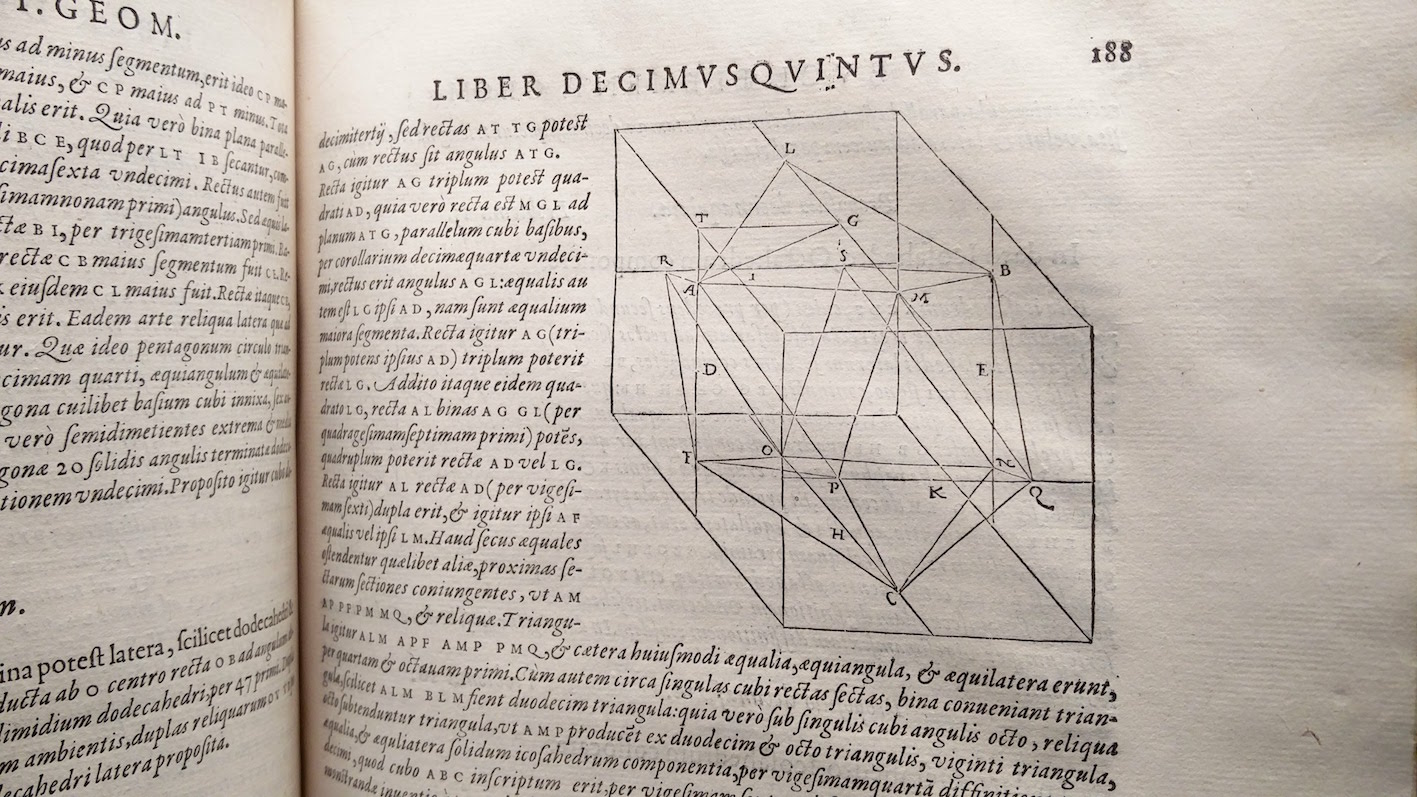
As well as his Book 16, Foix-Candale also added to his edition of Euclid a short treatise on regular and semi-regular polyhedra. This asked: what happens if you take a regular polyhedron, find the midpoint of each edge, and form a new polyhedron whose vertices are those midpoints? New solids; new diagrams to illustrate them; new theorems to investigate their properties. We now call solids of this class semi-regular: although all their edges are the same length, their faces are not all the same shape.
Together, Book 16 and the treatise on solids were a remarkable piece of work. Later editors and translators took them up: the famous 1570 English version of the Elements included a version of Foix-Candale’s Book 16. It was taken up in Latin by Christoph Clavius, whose schoolroom-tailored Elements of 1574 was possibly the most widely read version of the text in the seventeenth century. There was a Dutch translation, too. Editors were still printing Foix-Candale’s additions as part of the Elements as late as the 1750s.

Foix-Candale didn’t rest on his laurels. In 1578 he brought out a new edition of his Elements, this time with two more new books. Books 17 and 18 dealt, once again, with the manipulation and comparison of polyhedra, particularly the exoctahedron (with six squares and eight triangles for its faces) and icosidodahedron (twelve pentagons and twenty triangles). He looked exhaustively at the possibilities for placing these and other solids inside one another.
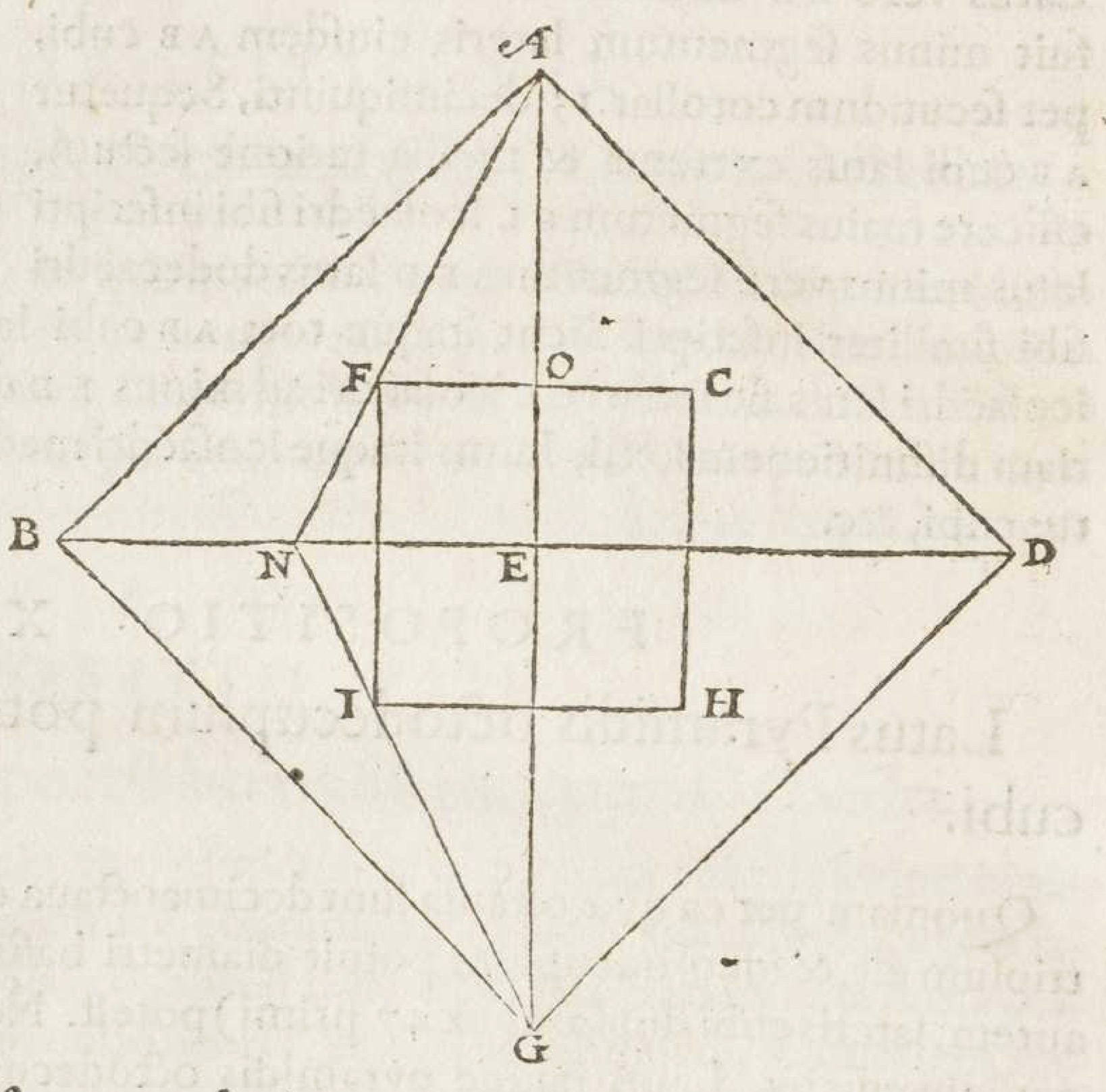
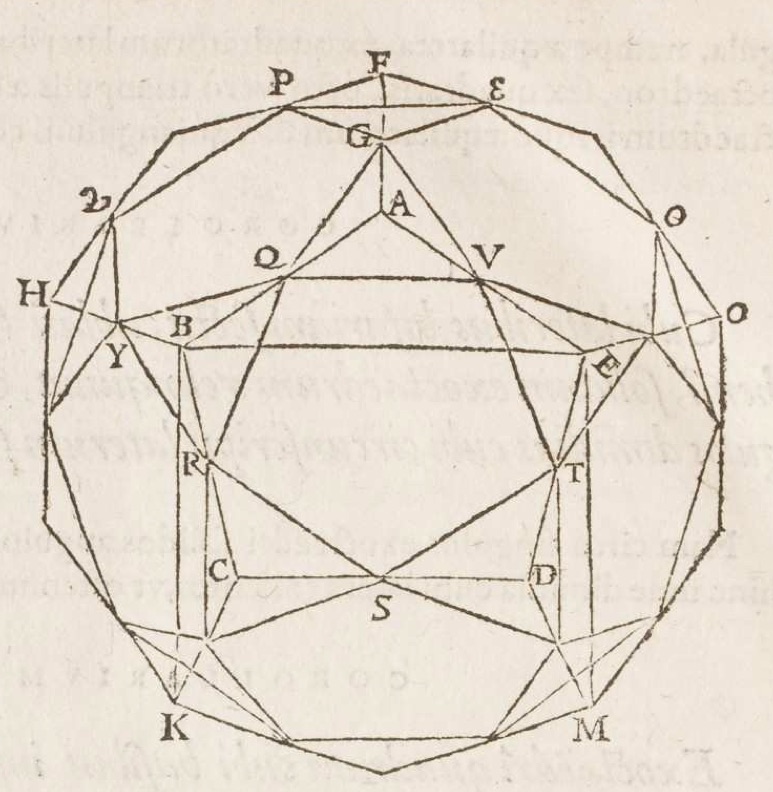
It’s a spectacular performance, full of such delights as this:
Proposition 33: A dodecahedron exceeds its inscribed icosidodecahedron by the volume of the prism whose base is an equilateral triangle erected upon the edges of both solids, and whose height is two ninths of the diameter of the dodecahedron.
Foix-Candale conveyed a real enthusiasm for the beauty – visual and intellectual – of his new polyhedra, these ‘most beautiful solids’, and his own geometrical imagination was evidently very fine, his ability to visualise and mentally rearrange three-dimensional shapes impressive indeed.
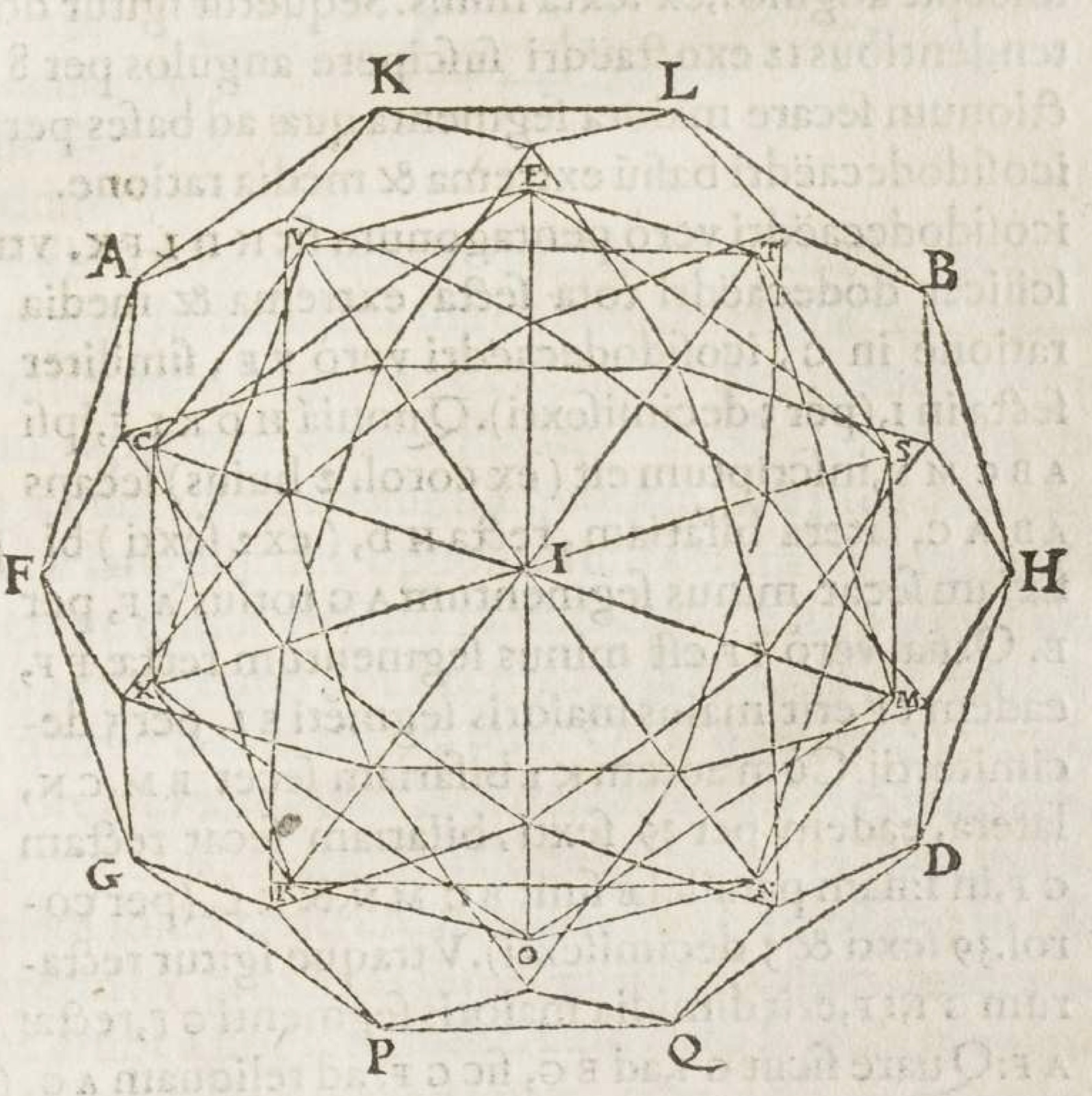
The French mathematician Marin Mersenne included a list of their propositions in his 1626 Synopsis mathematica, but ostensibly these new books travelled much less widely than his Book 16. Yet Foix-Candale’s interests found distinct echoes in the work of other mathematicians. In the 1620s René Descartes wrote his ‘Exercices pour les éléments des solides’, a more systematic examination of the semi-regular solids. Pierre Costabel, modern editor of that text, found evidence that Descartes may have taken inspiration from Foix-Candale’s work.
Again, Johannes Kepler’s famous geometrical model of the solar system – which we featured a few weeks ago – based on regular solids nested inside one another, was the kind of thing that delighted Foix-Candale. And, sure enough, Kepler referred to Foix-Candale’s Elements by name, and although he didn’t mention Book 16 (or 17 or 18), it’s hard to escape the feeling that the French bishop’s enthusiasm for placing regular solids inside one another must have had some resonance with the great astronomer.
In 1591 François de Foix-Candale founded a chair of geometry at the college of Guyenne. Three years later he died. His name has not become a famous one, and his posthumous reputation was affected by the confessional strife of the period. But his status as a geometrical author is neatly captured in the tomb designed for him in the 1630s by Hermann van der Hem: geometrical shapes were to surmount the sarcophagus itself – in the design some of them look much like his beloved semi-regular solids – while the praying figure of Foix-Candale looked down on the whole.

Further reading
J. Balteau, A. Rastoul and Michel Prévost, Dictionnaire de biographie française (Paris, 1929–), vol. 14, cols. 210–12.
Henry Delfour, ‘L’eau magistrale de Candale (un évêque d’Aire alchimiste)’, Bulletin de la Société de Borda (Dax) (1954), 192–204.
Paul Delaunay, ‘Un remède secret … épiscopal: L’eau magistrale de Caudale (un évêque d’Aire alchimiste), in Bulletin de la Société de Borda, 1954’, Revue d’histoire de la pharmacie 43/145 (1955), 96.
René Descartes, Exercices pour les éléments des solides: de solidorum elementis, ed. Pierre Costabel (Paris, 1987), 88–92.
P.J. Federico, Descartes on polyhedra: a study of the De solidorum elementis (New York, 1982).
J.V. Field, Kepler’s geometrical cosmology (London, 1988).
Fully digitised copy of the second edition (1578) from the Library of Max Planck Institute for the History of Science is available here.
